- Auto Tuning Video
- Kalman Filter Auto Tuning Kit
- Extended Kalman Filter Tutorial
- Kalman Filter Equations
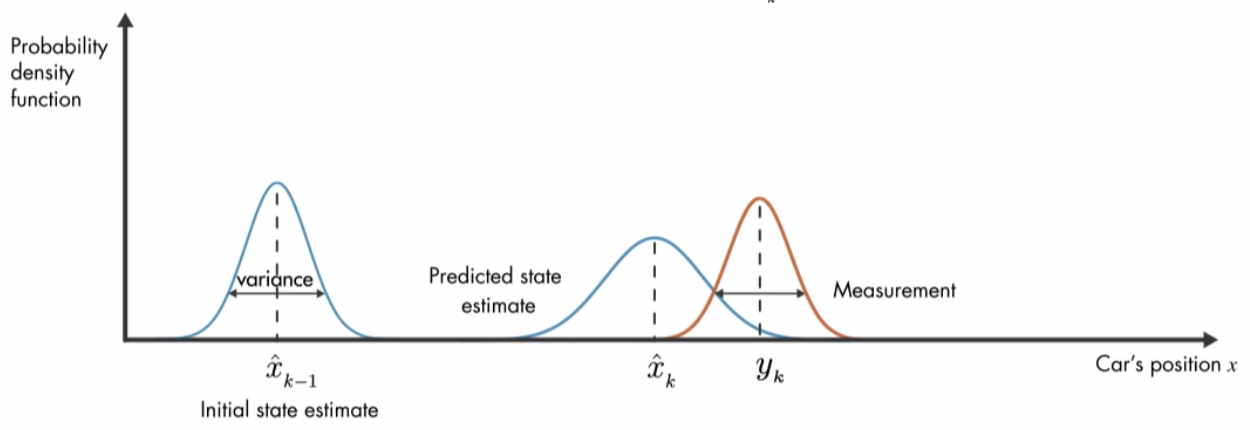
- System state (Fk, Hk, Qk and Rk) is known, the Kalman filter equations automatically guarantee statistical consistency. However, in many situations the model is not known precisely, and so the filter must be tuned. Filter Tuning Filter tuning is the process of selecting parameters to opti-mize performance. Consistency ensures two desirable.
- Design a Kalman filter to estimate the output y based on the noisy measurements yvn = C xn + vn Steady-State Kalman Filter Design. You can use the function KALMAN to design a steady-state Kalman filter. This function determines the optimal steady-state filter gain M based on the process noise covariance Q and the sensor noise covariance R.

Dec 17, 2019 While this work focuses mainly on auto-tuning of extended Kalman filters (EKFs), the BO framework can be readily extended to other related state space filtering algorithms. The rest of this paper is structured as follows. Sections II and III formally introduces an overview and problem statement for filter auto-tuning. Jul 04, 2019 Tuning of Extended Kalman Filters for Sensorless Motion Control with Induction Motor Abstract: This work deals with the tuning of an Extended Kalman Filter for sensorless control of induction motors for electrical traction in automotive.
This example shows how to perform Kalman filtering. Both a steady state filter and a time varying filter are designed and simulated below.
Problem Description
Given the following discrete plant
where
design a Kalman filter to estimate the output y based on the noisy measurements yv[n] = C x[n] + v[n]
Steady-State Kalman Filter Design
You can use the function KALMAN to design a steady-state Kalman filter. This function determines the optimal steady-state filter gain M based on the process noise covariance Q and the sensor noise covariance R.
First specify the plant + noise model. CAUTION: set the sample time to -1 to mark the plant as discrete.
Specify the process noise covariance (Q):
Specify the sensor noise covariance (R):
Now design the steady-state Kalman filter with the equations
The first output of the Kalman filter KALMF is the plant output estimate y_e = Cx[n|n], and the remaining outputs are the state estimates. Keep only the first output y_e:
To see how this filter works, generate some data and compare the filtered response with the true plant response:
To simulate the system above, you can generate the response of each part separately or generate both together. To simulate each separately, first use LSIM with the plant and then with the filter. The following example simulates both together.
Next, connect the plant model and the Kalman filter in parallel by specifying u as a shared input:
Finally, connect the plant output yv to the filter input yv. Note: yv is the 4th input of SYS and also its 2nd output:
The resulting simulation model has w,v,u as inputs and y,y_e as outputs:
You are now ready to simulate the filter behavior. Generate a sinusoidal input vector (known):
Generate process noise and sensor noise vectors:
Now simulate the response using LSIM:
Compare the true response with the filtered response:
As shown in the second plot, the Kalman filter reduces the error y-yv due to measurement noise. To confirm this, compare the error covariances:
Covariance of error before filtering (measurement error):
Covariance of error after filtering (estimation error):
Time-Varying Kalman Filter Design

Auto Tuning Video
Now, design a time-varying Kalman filter to perform the same task. A time-varying Kalman filter can perform well even when the noise covariance is not stationary. However for this example, we will use stationary covariance.
The time varying Kalman filter has the following update equations.
First, generate the noisy plant response:
Kalman Filter Auto Tuning Kit
Next, implement the filter recursions in a FOR loop:
Now, compare the true response with the filtered response:
The time varying filter also estimates the output covariance during the estimation. Plot the output covariance to see if the filter has reached steady state (as we would expect with stationary input noise):
Extended Kalman Filter Tutorial
From the covariance plot you can see that the output covariance did reach a steady state in about 5 samples. From then on, the time varying filter has the same performance as the steady state version.
Compare covariance errors:
Covariance of error before filtering (measurement error):
Covariance of error after filtering (estimation error):
Verify that the steady-state and final values of the Kalman gain matrices coincide:
Comments are closed.